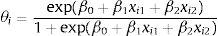This work attempts to provide a model to predict the development of osteonecrosis (ON) in individuals with systemic lupus erythematosus (SLE) using pharmacological, demographic, and psychoactive factors.
MethodA review of the literature was conducted to construct a survey administered across Chile to individuals with SLE during a period of three weeks. This work used a sample size of 46 de-identified data records. Two Bayesian logistic regression models were created, with non-informative prior and informative prior distributions, and a random forest model was done for comparison. All models were cross-validated.
ResultsThe significant variables used were mean corticosteroids per day (mg) and tobacco use. The random forest model provided good accuracy and sensitivity, but low specificity. Bayesian logistic regression with prior information increased the specificity.
ConclusionsThis work determined that the use of corticosteroids and tobacco are significant variables to predict ON. Using prior information provides good accuracy, specificity, and sensitivity to the prediction. Further studies need to be conducted to validate the model using a testing set.
Este trabajo busca determinar un modelo predictivo de desarrollo de osteonecrosis (ON) en individuos diagnosticados con lupus eritematoso sistémico (LES) utilizando factores farmacológicos, demográficos y psicoactivos.
MétodoSe realizó una revisión bibliográfica para construir una encuesta, la cual fue administrada a individuos con LES a lo largo de Chile durante un periodo de 3 semanas. En este trabajo se utilizó una muestra de 46 registros de datos no identificados. Se desarrollaron 2 modelos de regresión logística bayesiana con información a priori no informativa e informativa, y también se desarrolló un modelo comparativo utilizando bosques aleatorios. Los modelos fueron validados usando validación cruzada.
ResultadosSe usaron las variables significativas promedio de corticosteroides por día (mg) y consumo de tabaco. Bosques aleatorios provee una precisión y sensibilidad alta, pero una baja especificidad. La regresión logística bayesiana con información a priori incrementó el valor de la especificidad.
ConclusionesEste trabajo ha determinado que el uso de corticosteroides y tabaco son variables significativas para predecir ON. Usando información a priori arroja buenos resultados en precisión, especificidad y sensibilidad en la predicción. Se requieren realizar más estudios aumentando el tamaño de la muestra para validar el modelo usando un conjunto de prueba.
Patients with systemic lupus erythematosus (SLE) have a higher incidence of a variety of secondary associated diseases than the general population.1 These comorbid diseases arise from the SLE itself or because of the use of some medications to treat it.2–4 A secondary disease associated with SLE is osteonecrosis (ON), whose prevalence varies widely, from 4% to 40% in patients with lupus.4,5 ON is considered the main secondary disease that causes morbidity in patients with SLE.5
Several studies aimed to determine predictive factors of ON in patients with SLE2,4,6–10; however, none have attempted to develop a predictive model, which is the next step after determining the significant variables. A predictive model is a tool that supports the decision-making of the providers to apply proper treatments considering the uniqueness of each patient. The objective of this work is to develop a predictive model to determine if an individual suffering from SLE can also be diagnosed with ON using pharmacological, demographic, and psychoactive factors.
Materials and MethodsData CollectionThe literature was reviewed to identify factors that are deemed to be related to the development of ON in SLE patients. Data for the Chilean population was collected through an online survey, which was developed based on findings from the literature, health care providers, survey development experts, and individuals with SLE. The effort resulted in an 89-question instrument distributed in four sections: general information, information about the SLE, healthy lifestyle, and information about the ON. The survey was administered through a confidential online platform across Chile for a period of three weeks during December 2015. Each participant was required to read and sign a form providing consent. The process resulted in 46 de-identified records where 15.22% developed ON and 98.21% were women.
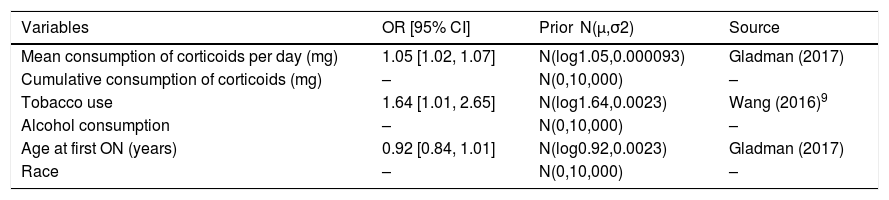
Development and Evaluation of a Predictive ModelThe de-identified data were used to create two models using a Bayesian logistic regression approach. The response variable was the occurrence of the first ON (1: individual developed first ON, 0: individual did not develop ON). The explanatory variables analyzed were mean consumption of corticosteroids per day (mg), cumulative consumption of corticosteroids (mg), tobacco use, alcohol consumption, age at first ON, and race (Mapuche—indigenous—origins or not). Models were validated using leave-one-out cross-validation. The first model used a non-informative prior multivariate normal distribution for the parameters’ betas, specifically, βi∼N(0,10,000), j=0,1,…,6. The second model used a multivariate normal distribution, mixing non-informative and informative prior normal distributions recently available in the literature (Table 1). The priors were selected based on the significance of the variables in the studies (α=0.1): mean consumption of corticosteroids per day, with a P-value equal to .0002; tobacco use, with a P-value equal to .05; and age at first ON, with a P-value equal to .08.
Prior Information for Bayesian Logistic Regression.
| Variables | OR [95% CI] | Prior N(μ,σ2) | Source |
|---|---|---|---|
| Mean consumption of corticoids per day (mg) | 1.05 [1.02, 1.07] | N(log1.05,0.000093) | Gladman (2017) |
| Cumulative consumption of corticoids (mg) | – | N(0,10,000) | – |
| Tobacco use | 1.64 [1.01, 2.65] | N(log1.64,0.0023) | Wang (2016)9 |
| Alcohol consumption | – | N(0,10,000) | – |
| Age at first ON (years) | 0.92 [0.84, 1.01] | N(log0.92,0.0023) | Gladman (2017) |
| Race | – | N(0,10,000) | – |
OR: odd ratio; CI: confidence interval.
The likelihood contribution of each individual was binomial. The posterior distribution was simulated using Markov chain Monte Carlo (MCMC) and the random walk metropolis (RWM) algorithm implemented in R software. The total of iterations was 10,000,000 with a burn-in of 9,000,000 iterations. The threshold was determined using the complete sample size through the receiver operating characteristic (ROC) curve, maximizing the summation of the specificity and sensitivity. The analysis of significance for the first and second models used 90% and 95% credible intervals (CI), respectively.
The performances of the Bayesian models were compared to the non-parametric random decision forest model for accuracy, sensitivity, and specificity. The optimal input variables were determined using the tuneRF function in R, minimizing out-of-bag (OOB) errors. The number of trees was determined screening from 1 to 1000 trees, plotting the values against the OOB errors. The random decision forest splits were performed using the Gini index.
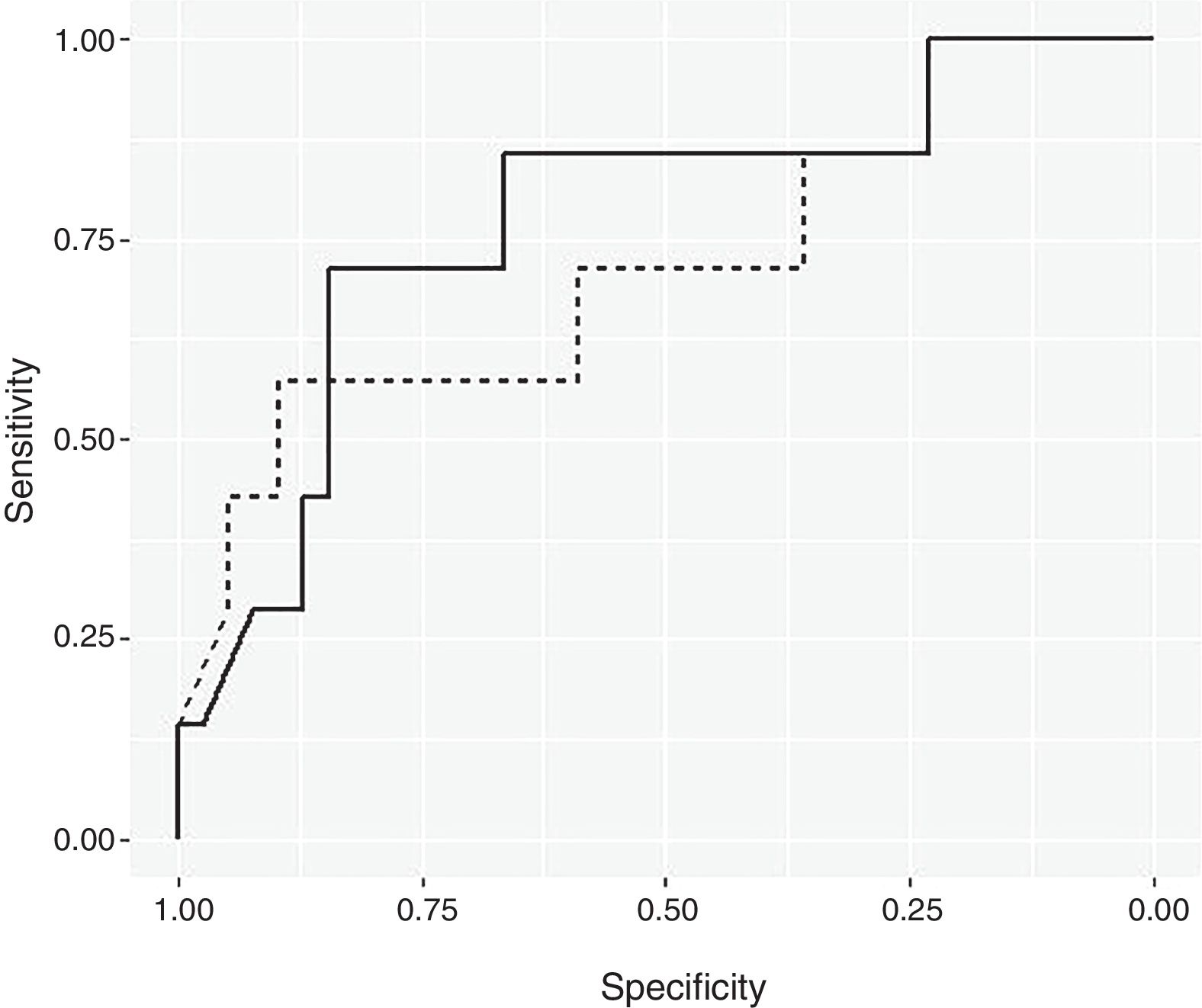
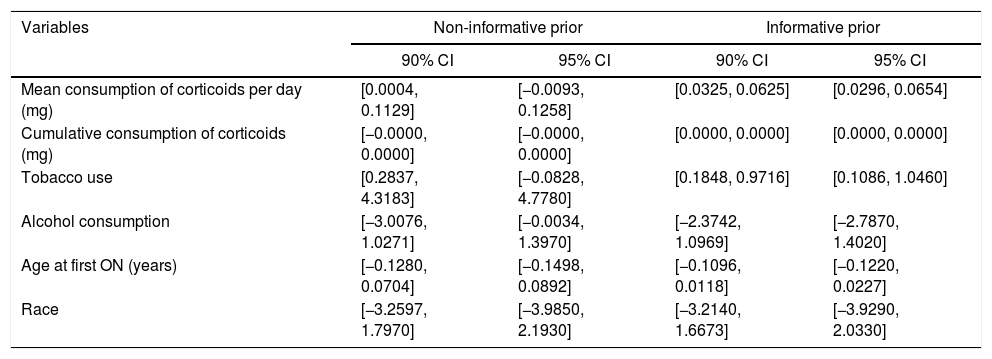
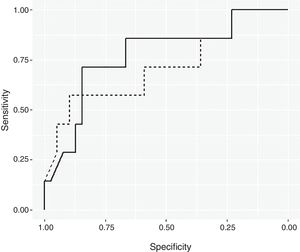
ResultsBayesian Logistic Regression ModelsUsing a non-informative prior distribution and a 95% CI, none of the variables seemed to be significant (Table 2). With a 90% CI, the variables of mean consumption of corticosteroids per day and tobacco use were both significant. Using prior information, the same variables are significant with a 95% CI. These two variables were used to create the Bayesian logistic regression model. Fig. 1 shows the ROC curve for the non-informative (smooth line) and informative (dotted line) Bayesian logistic regression models. The threshold for the non-informative prior model was 0.1819, and the model for the informative prior was 0.2187. These values were used to validate the respective models.
90% and 95% Credible Intervals For Non-informative and Informative Prior.
| Variables | Non-informative prior | Informative prior | ||
|---|---|---|---|---|
| 90% CI | 95% CI | 90% CI | 95% CI | |
| Mean consumption of corticoids per day (mg) | [0.0004, 0.1129] | [−0.0093, 0.1258] | [0.0325, 0.0625] | [0.0296, 0.0654] |
| Cumulative consumption of corticoids (mg) | [−0.0000, 0.0000] | [−0.0000, 0.0000] | [0.0000, 0.0000] | [0.0000, 0.0000] |
| Tobacco use | [0.2837, 4.3183] | [−0.0828, 4.7780] | [0.1848, 0.9716] | [0.1086, 1.0460] |
| Alcohol consumption | [−3.0076, 1.0271] | [−0.0034, 1.3970] | [−2.3742, 1.0969] | [−2.7870, 1.4020] |
| Age at first ON (years) | [−0.1280, 0.0704] | [−0.1498, 0.0892] | [−0.1096, 0.0118] | [−0.1220, 0.0227] |
| Race | [−3.2597, 1.7970] | [−3.9850, 2.1930] | [−3.2140, 1.6673] | [−3.9290, 2.0330] |
CI: credible interval.
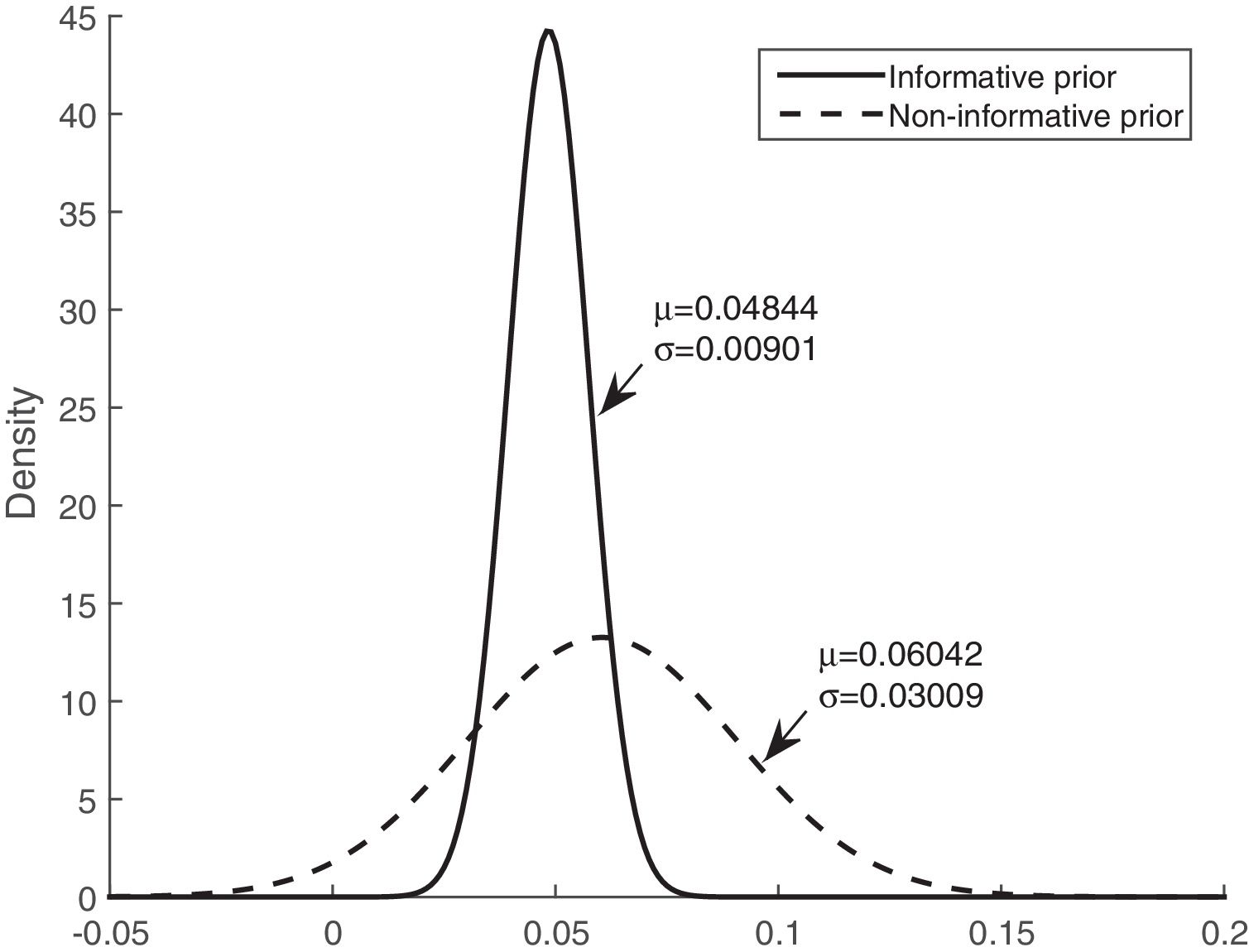
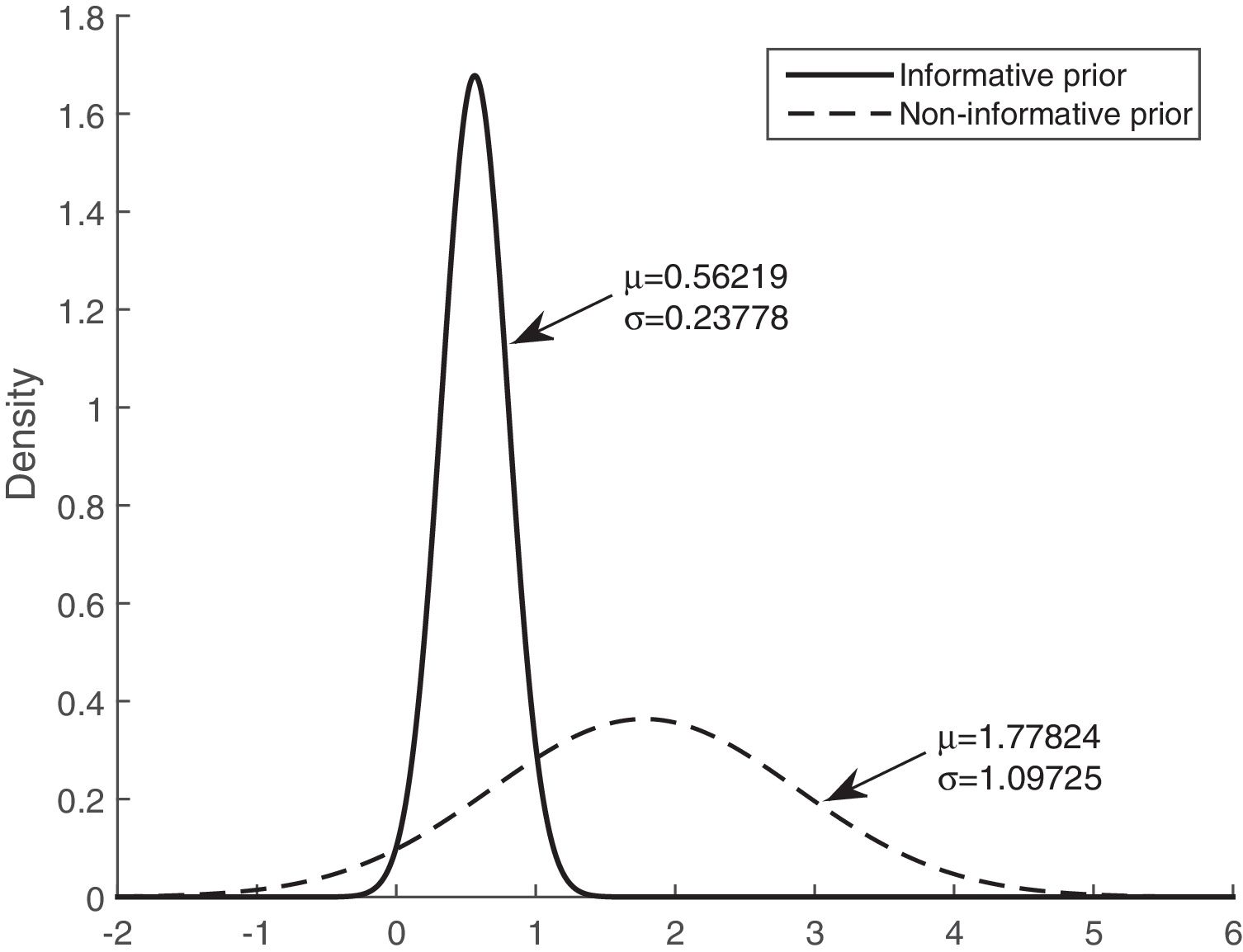
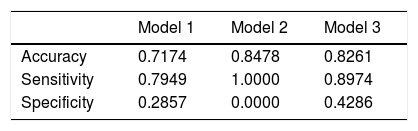
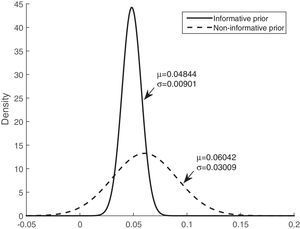
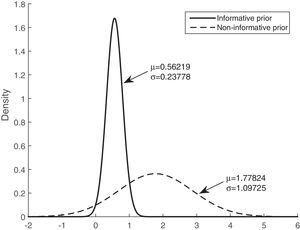
Table 3 shows that the sensitivity, specificity, and accuracy were higher for the Bayesian logistic regression models with prior information than for the model with non-informative prior information. The mean of the posterior distributions for the informative prior provides the estimators of the parameters. The estimators, considering the mean and the standard deviation (mean±SD), are as follows: intercept (βˆ0) −3.300±0.534, mean of corticosteroids per day (βˆ1) 0.048±0.009, and tobacco use (βˆ2) 0.562±0.238.
Accuracy, Sensitivity, and Specificity of the Model.
| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| Accuracy | 0.7174 | 0.8478 | 0.8261 |
| Sensitivity | 0.7949 | 1.0000 | 0.8974 |
| Specificity | 0.2857 | 0.0000 | 0.4286 |
Model 1: Bayesian logistic regression with non-informative prior.
Model 2: Random decision forest.
Model 3: Bayesian logistic regression with informative prior.
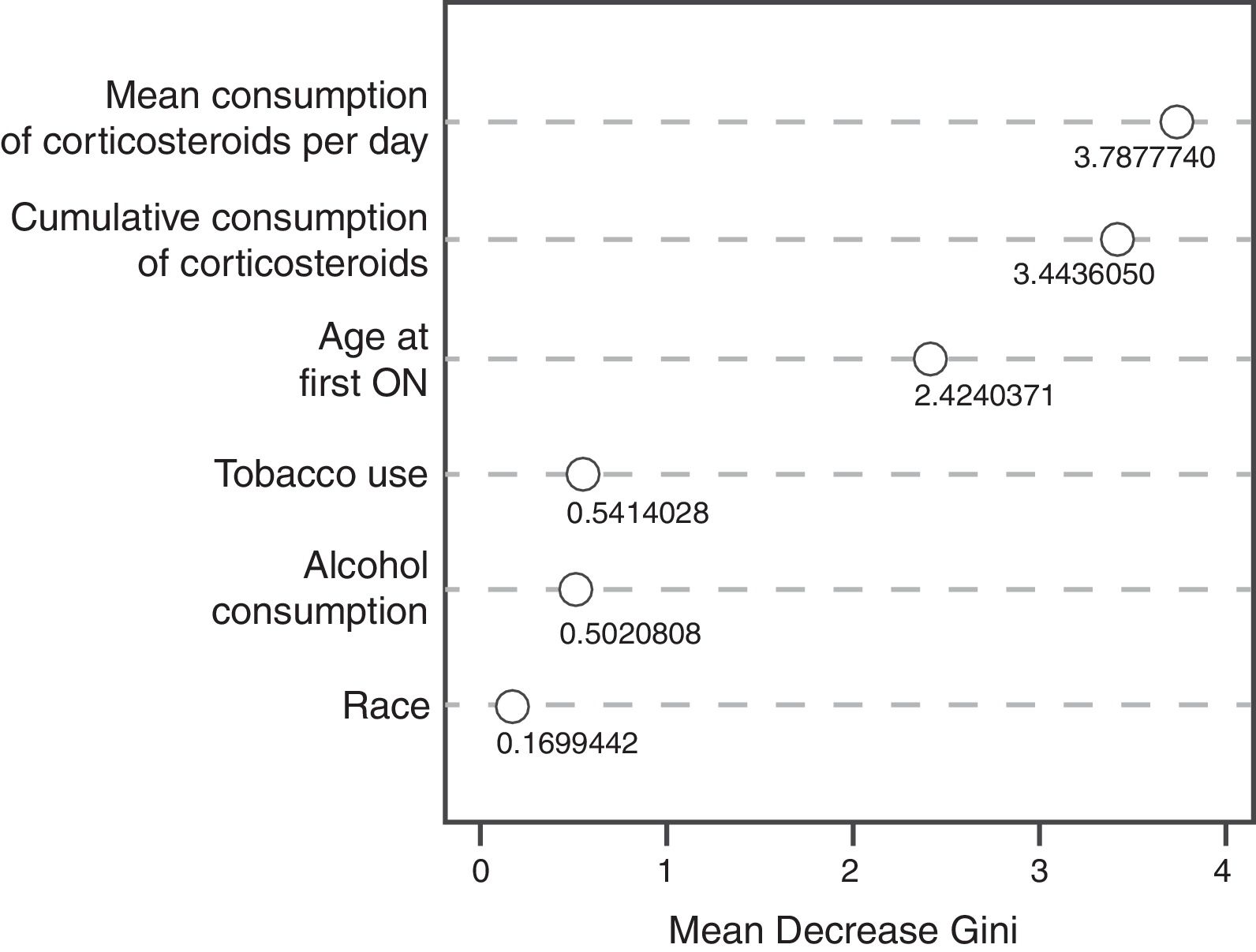
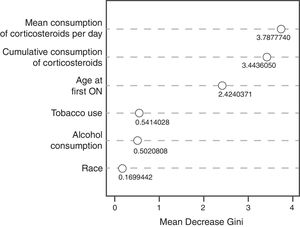
The random decision forest model used 85 trees and two input variables. The accuracy of the random forest model (0.8478) was higher than the Bayesian logistic regression model with prior information. The sensitivity was the highest (1.0), but the specificity was the lowest (0.0), which means that the model was unable to predict the development of ON (Table 3). The variable importance plot (Fig. 2) displays that the mean corticosteroids per day led to the largest mean decrease in Gini impurity (3.7878).
DiscussionVarious studies have established that patients who receive high doses of corticosteroids are susceptible to developing ON in certain areas of the body.2,4,6,10,11 Patients with SLE are administered high doses of corticosteroids in their therapies for long periods, and therefore, they are at risk of developing ON. However, there is uncertainty whether the cumulative doses and the duration of treatment with corticosteroids or the use of large doses of corticosteroids on a daily basis are the contributing factors to development of the disease. Therefore, it is not surprising that a variable related to corticosteroids is significant in the Bayesian models and influences the prediction power in random forest. In addition, it is not unusual that tobacco use was significant in the models because studies have related ON with non-corticosteroid factors such as tobacco use, alcohol consumption, age, gender, and race, among others.6,7,9
Figs. 3 and 4 show the comparison of the posterior distributions for the parameters of the Bayesian models with prior and non-prior distribution. Fig. 3 depicts the posterior distribution of the regression coefficient for mean corticosteroids per day, and Fig. 4 shows the posterior distribution of the regression coefficient for tobacco use. There is a significant reduction in the variance in the models with prior information. The variance of the posterior distribution for mean corticosteroids per day decreased in 91%, and the mean decreased in 20%. The estimators of the variable mean corticosteroids per day for the model with prior distribution and the model without prior distribution are close. This highlights the relevance of this factor. A similar reduction occurred with the posterior distribution for tobacco use: the variance decreased in 95.2%, and the mean decreased in 68.5%.
With regard to the best performance model—Bayesian logistic regression model with prior information—the probability of developing ON, θi, is calculated using Eq. (1), where i is the individual. Since the coefficient for mean corticosteroids per day and for tobacco use are positive, the probability of developing ON will also increase if any of these variables increase.
Specifically, if the explanatory variable, mean corticosteroids per day, increases by 1mg, and the variable tobacco use keeps constant, the ratio between the probability that the individual develops ON and the probability that the individual does not develop ON increases by e0.048⋅(≈1.049). Likewise, if an individual consumes tobacco and the other variable is held constant, the ratio increases in e0.048⋅(≈1.754).
The use of the preceding information is one of the main advantages of the Bayesian approach, which is not possible with random forest and other methods. In addition, the estimators of the parameters calculated in this study provide prior information for future works in this matter. Although random forest produces a higher accuracy than Bayesian logistic regression with prior information, it is non-trivial to interpret and analyze, and it seems to present problems when the sample size is small. The Bayesian approach provides better interpretability and inferences. In summary, this work explores the opportunity of better supporting a provider's decision when treating individuals with lupus. The use of this tool along with other outcome metrics, specifically, measurements of disease activity (e.g., SLE diseases activity index – SLEDAI) could further support the providers, since a higher disease activity score appears associated with the incidence of ON in individuals with SLE.12
This study has three main limitations. First is the possibility of bias due to the auto report nature of the data because the data was extracted using a survey rather than clinical records. Second, the type and depth of clinical questions on the survey because the individuals responding are not able to address complicated clinical questions. Third, the sample size, which does not allow for more in-depth training, testing, and validation.
Conflicts of InterestThe authors declare no conflicts of interest.